Sparta/TIL

[TIL] 선택정렬, 버블정렬 with Javascript

jskim4695 2024. 4. 9. 12:25
in place 알고리즘은 자료구조를 추가로 사용하지 않고 입력을 변환하는 알고리즘이다. 종류는 다음과 같다.

 

1. 선택정렬

정렬되지 않은 데이터들에 대해 가장 작은 값을 찾아 가장 앞의 값과 교환해나가는 방식이다. n번째 회전이 끝날 때마다 앞에서 n번째 데이터의 위치가 정해진다.

 

1) 과정

i. 주어진 리스트중 최솟값을 찾는다.

ii. 그 값을 맨 앞에 위치한 값과 교체한다.

iii. 맨 처음 위치를 뺀 나머지 리스트들을 같은 방법으로 교체한다.

 

2) Big O

O(n^2)의 시간복잡도를 지닌다. 또한 이미 정렬되어 있는 배열을 탐색해도 마찬가지다.

매번 정해진 자리에 올 수 있는 최솟값을 찾아야하기 때문에 성능이 매우 떨어진다.

단순한 편이며 사용할 수 있는 메모리가 제한적일 경우 사용시 이점이 있다.

 

//선택
function selectionSort(array) {
  for (let i = 0; i < array.length; i++) {
    let minIndex = i;

    for (let j = i + 1; j < array.length; j++) {
      if (array[minIndex] > array[j]) {
        minIndex = j;
      }
    }

    if (minIndex !== i) {
      let swap = array[minIndex];

      array[minIndex] = array[i];

      array[i] = swap;
    }

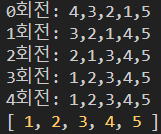
    console.log(`${i}회전: ${array}`);
  }
  return array;
}
console.log(selectionSort([5, 4, 3, 2, 1]));

 

선택정렬 결과

 

 

2. 버블정렬

쌍대비교와 비슷한데, 거품이 일어나듯 연쇄적으로 자기자리를 찾아간다. 데이터를 두개씩 묶어서 비교한 수 큰 값이 오른쪽으로 가도록 자리를 바꿔가며 큰 데이터를 오른쪽으로 민다. n번째 정렬 회차가 끝나면 뒤에서 n번째 자리의 데이터가 확정된다.

 

1) 과정

i. 왼쪽부터 인접한 데이터 두개를 찾는다.

ii. 두 수를 비교하여 큰 쪽을 오른쪽으로 보낸다.

iii. 1회차 동안 반복한다.

 

2) Big O

정렬이 하나도 안 되어 있는 경우 각 자리를 찾기 위해서 n번의 순회를 해야 하고, 또 n번의 회전동안 요소의 개수만큼 또 순회를 해야한다. O(n^2)의 시간 복잡도를 가진다. 그에 반해 이미 정렬이 되어  있는 경우는 한번의 순회로 정렬 여부를 알 수 있기 때문에 O(n)의 시간복잡도를 가진다. 즉, 정렬의 정도에 따라 시간복잡도가 달라진다. 가장 큰 단점은 자료의 개수가 많아질수록 성능이 매우 떨어진다는 점이다. 최악의 경우 O(n^2)가 걸리기 때문이다.

 

function bubbleSort(array) {
// i가 0~array.length 범위에서 for문이 한번 돌고
  for (let i = 0; i < array.length; i++) {
    let swap;
// j가 0~array.length-1-i 범위에서 for문이 다시 돈다.
// 마지막 데이터를 포함하지 않고, 각 회전이 끝날 때마다 마지막 데이터의 정렬이 끝나기 때문
    for (let j = 0; j < array.length - 1 - i; j++) {
// 인접한 두 값을 뽑아 비교한다.
      if (array[j] > array[j + 1]) {
        swap = array[j];
        array[j] = array[j + 1];
        array[j + 1] = swap;
      }
    }
// 만약 각 회전을 끝내고 swap 변수가 undefined라면 for문을 종료
    console.log(`${i}회전: ${array}`);
    if (!swap) {
      break;
    }
  }
  return array;
}

console.log(bubbleSort([5, 4, 3, 2, 1]));

버블정렬